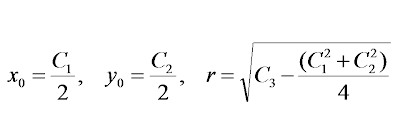Listening In with AWSMCBB

Lets listen in on a practice set with the All White Suburban Middle Class Blues Band.

Motto:  "We Play The Blues 'Cause We Paid Our Dues (and we got a tax receipt of course.)"


First up is an old original Fleetwood Mac number, "Heart Beats Like a Hammer" from their debut album imaginatively titled, "Fleetwood Mac."  This goes back to the days when Fleetwood Mac was still strictly a Blues Band, before the girls came to play.



(If there is a problem with playback, click "pause" for a few seconds and allow it to buffer.)


Next we have a go at Otis Rush's "All Your Love" which has also been covered by the likes of John Mayall and The Bluesbreakers (featuring Eric Clapton), Aerosmith, Stevie Ray Vaughan, The Steve Miller Band, and now of course The AWSMCBB. That's us.




Finally, one of our old standbys, "Tore Down" by the ineffable T-Bone Walker (aka Aaron Thibeaux Walker, 1910 - 1975). What does 'ineffable' mean? I assume it means "not able to be effed." So we'll do our best not to, this time.




The AWSMCBB is:

Tim (guitar & vocals)
Nick (bass)
Paul (drums) and
John (piano & organ).

Our music is NOT SOLD IN ANY STORES!   Gee, I wonder why.

The Most Fun I Ever Had!

The most fun I ever had using Mathematics to solve an original problem ('original' meaning I had to work it out for myself without any help) was back while I was working as a junior engineer/floor sweeper at Bently Nevada Corp.  To make measurements of rotor shaft position within a plain sleeve bearing, everyone up until that time would just "guesstimate" the limits of motion that indicated the bearing clearance.  I decided there would soon be a better way.

With just a few measurements of rotor position in X and Y (as shown here), can you construct the most likely circle out of these points?  It seems like it should be easy, but how can we be certain of getting the right result?  And how do you teach a computer to do this without your visual help?

We could take any three points and use the famous Three-Point Formula for a circle, then solve it algebraically for the radius and  X - Y coordinates of the circle's center. But which three points do you use?  And remember, these are measurements that always have some random error in them.  If you look closely, these points do not actually fall on an exact circle.

One solution would be to take every possible combination of three points, determine the circle's parameters, then make an average of all the possibilities.  But there is a better way.

If there are 47, 102, 18 or any other number of data points we'll call N, then the raw data are an N-dimensional object that can only be perfectly represented using all N dimensions.  But common sense tells us that most of those dimensions are unnecessary, because it really only takes 3 numbers to represent a circle: the value of its radius, and the X and Y coordinates of the circle's center.  If all these data points were exactly on a perfect circle, they would not be N independent entities, because there would be a very concise rule dictating where the points were allowed to be.  In reality, though, they won't all line up perfectly (see above), so we need a way of determining what is statistically the best circle described by the data.

Mathematically the problem is how to minimize the distance between every point and some proposed circle by adjusting the circle's position and radius.  The optimization parameter used is the sum of the square of how far off the circle each data point is.  Such an optimized circle will be known as the "least squares best-fit."

The question really boils down to this:  how do you smoosh an N-dimensional object (a data set with N points) into just three pieces of information? And how can we be certain that they represent the optimum best fit?  It's easy, if you know how to use a handy little thing called The Perfectly Normal Equations.

Don't panic - this is a Perfectly Normal Equation.

Many textbooks refer to these as simply the "Normal Equations," and this omission betrays the authors' ignorance regarding the real origin of the name, as well as their deplorable lack of familiarity with the works of Douglas Adams.  They assume it's because "normal" is another word for "orthogonal" meaning "perpendicular to each other."  In other words, no combination of any of the equations will adequately work as a replacement for any one of them.

While that is technically true, the real reason for the name "Perfectly Normal Equations" is so that when people see them, they will be prepared to accept these equations as "perfectly normal" and will not freak out and alert the Authorities, or do something equally dramatic and ill-advised.

The one slightly disconcerting thing about the Perfectly Normal Equations is that there appears to be only one of them.  And, they are not actually equations, but more like the pattern or formula one uses to create the specific Perfectly Normal Equations for any given situation.   The elegantly simple statement shown above is really a set of instructions for how to combine something called "Basis Functions" into Perfectly Normal Equations which will then perform all kinds of wonderful feats.

Actually, the only wonderful thing they do is cast mathematical shadows, the way a 3-dimensional object casts a 2-dimensional shadow on a wall.  But in this example, it's an object with hundreds of dimensions, and we want to "flatten" it down to just three pieces of information: the radius and two center coordinates of a circle.  But that is wonderful enough for me.  I am easily amused.

So.  What are the Basis Functions of a circle?  Whoops - they didn't teach us that in school, did they.  That is the part I had to figure out all by myself, and this is the stroke of jeenyous that leads to this amazing solution to a tricky problem.

First, what does the word "circle" really mean?  To get specific enough to be useful, we have to define it as those points on a plane that are all exactly a certain distance (called the radius) from one point (called the center).  We can use good ol' Pythagoras' formula for the distance between points.  And that is the rule or statement that defines what is a circle.


But not every circle is centered at point 0,0, and so we have to allow for the possibility that the center is located at some point (x_o, y_o) instead:

General Equation of a Circle

Just because I felt like trying something different, I decided to re-organize this equation to make it look like a polynomial in X and Y being equal to a function of X and Y.  The inelegant result is this:

The John S. Jacob form of the Circle Equation

And now the AHA! moment.  In that form, a circle looks exactly like something that might fit in the Perfectly Normal Equations:

If you've ever sweated through a math class, you might be experiencing some disappointment right here.  "What?  That's it? x, y and 1 are your basis functions?  That's LAME!"  Well, to be honest I expected something more complicated too.  But that's how it comes out.  Some days there's a fine line between genius and idiocy.

Now the Perfectly Normal Equations can be written out in all their salacious details.  I will spare your bandwidth here, but if you really want to see them in their exposed glory, contact me and I'll send you a pdf.

Three basis functions means there are three Perfectly Normal Equations, each containing three terms.  That forms a 3x3 grid, which itself makes a new kind of number that obeys a fancy sort of arithmetic called matrix algebra.  All we need to do is find the inverse of that matrix to solve for the three unknown constants, C. Why?  What will knowing the three C's give us?

Aha!  Another flash of genius.  The three C's are enough information to puzzle out the three exact values of  x_o, y_o and r.  And THAT tells us the absolute best circle that fits the entire data set.

Anyone can do this, because if you're reading this, you personally have access to about 1 million times the computing power needed to perform this calculation in less than a second. And the chances are very good that you have unknowingly already used Perfectly Normal Equations.

If you ever took a science, economics, business math or statistics class, you may have used Linear Regression to find a straight trend line that fits some data.  Did you ever stop to wonder where they first got the formula for doing Linear Regression?  No, of course you didn't.  Because you, unlike me, are Perfectly Normal.

Linear Regression is nothing more than the Perfectly Normal Equations using x and 1 as basis functions and a comparatively infantile 2x2 matrix inversion.

That's how Perfectly Normal they are!

Not to brag, but I've used the Perfectly Normal Equations and a 10x10 matrix inversion to save my former employer mega $$$ and heaps of space on a circuit board.  Talk about tough, I used up a whole pad of paper and an entire pencil working it all out.

But they were really nice about it - they bought me another one.










Exactly where did I learn all this stuff?  Oh, books, mostly.  This one by Kincaid and Cheney is a really good one:

My Reaction (Har!) to the Nuclear Debate

I crack myself up. Seriously, though. it has been observed that there is not one major global problem that could not be significantly diminished, if not altogether eliminated, by only one minor change that is entirely within every individual's reach.  Just one simple choice could solve the problems of Global Warming, peak oil, disease, poverty, war, urban overcrowding, crime, environmental degradation, extinction of species, water shortages, the Great Pacific Garbage Patch, traffic congestion, overflowing landfills, and American Idol.

That powerful but simple solution is this one easy-to-understand idea:  fewer humans on the planet.  That isn't likely to happen any time soon, since making more humans is just so gosh darned fun.

(Keeping one's pants fully in the "on" position is coincidentally also the solution to a surprising number of non-global, personal, legal, financial and medical problems, but that's another post.)

There is no question that we are going to run out of cheap energy relatively soon.  Yet everyone I've talked to recently still seems fully committed to reproducing themselves as many times as possible.  An alternative source of energy is needed if only to provide the illusion that everything is going to be OK while we continue to breed like teenage rabbits in a carrot silo.

This is the point at which some shill from the energy company pipes up and says, "Did you know that just one tiny kilogram of environmentally-friendly non-CO2-emitting Uranium replaces about two thousand TONS of horrible, disgusting coal?  With nuclear power, you humans could continue having sex for thousands of years to come!"

This raises two vitally important questions.  1) What happens after that?  2) Are you a robot, or an alien, or an alien robot?

His answer is, "Mumble mumble mumble mumble mumble."

"WHAT WAS THAT YOU SAID?"

"I said you're right back where you started, plus you have a bunch of, um, radioactive waste to deal with.  Hey, but at least it was cheaper than solar power!"

Is it really?  Not when you include ALL the costs.  Storage of the waste in particular is a blank-check expense.  Nuclear waste  is composed of an unmanageable jumble of highly hazardous substances all mixed together.  It really isn't worth mucking around with, because it's a never-ending game of whack-a-mole.  Just when you figure out how to neutralize one radioactive isotope, it decays into several new ones.  No, with this sort of muck, there's no point mucking about.  Best just put it someplace, and then never ever go there again.

That's why the Australian Goobermint has recently taken steps towards the establishment of a permanent nuclear waste storage facility (a shed, actually).  They considered the question of where to keep all this muck, and came up with the answer:  out in the middle of nowhere at a place called (and I am NOT making this up) -  Muckaty Station.

But how much is this going to cost?  Including a couple of rent-a-cops who will stand guard and prevent terrorists from stealing the glowing deadly muck, I optimistically estimate that it will cost 5 cents per day.  I'd make it 1 cent per day to be even more optimistic, but 5 cents is the lowest you can go in Australia, they having wisely done away with all the one-cent coins years ago. (Are you reading this, America? It works, it saves lots of time and tons of federal money.)

So, how many days will the radioactive waste need to be stored?  And keep in mind that we're going to be making more of it as time goes by.  It works out to be . . . infinity days.   Now, what is our very optimistic 5 cents per day times our frankly realistic infinity days?  Whoops - this calculator doesn't go that high.

-            -             -

Until someone figures out an affordable and politically acceptable means of dealing with nuclear waste, I say that it is NOT CHEAPER than solar power or any other form of energy.  Until that problem is solved, I maintain that the actual cost of nuclear power is infinity.

Plus thorium.  I meant to work that into this post somehow.  We should be looking at thorium fuel cycles, not uranium, because you can't make weapons out of it, it's inherently stable and stops reacting when you get hit by tsunamis, and the waste is slightly less nasty.  So, there it is.  The answer to all our problems is to stop having sex, and use more thorium.

A Complicated Day

March 10 is always a complicated day for me, for complicated and varied reasons.
For example, on this day in 1957, a man named Mohammad bin Awad bin Laden became a father.  Again.  He managed to do this a total of 54 times in his life, with 22 different wives.  See, now there's a guy who understood about putting all your eggs in one basket.  One smart man, if you ask me.  Obviously, not all your kids will turn out great, but what a disappointment little Osama turned out to be!

It's also the day  in 1940 that Ray Norris, famous Oklahoma mechanic and truck driver, became a dad for the first time when little Carlos was born.  Ray was destined for heartache however when the boys' mother moved to California, taking Ray's sons with her.  When Chuck Norris breaks someone's heart, it stays broken.

Graham Farmer, born on March 10th.

James Gerald Ray became a father on this day, as well.  In 1928.  We know so little about him, though.  Did he ever wonder, for example, where he went wrong with his son, the low-life assassin James Earl Ray?

It's not all bad news, though.  In 1935 on this day, a man named Farmer had a son nicknamed Polly.  This lad became the most famous Australian Rules Football player in history, Graham Farmer.  In America, he'd probably be the equivalent of Ronald Reagan or something.  Today, there's a freeway in Perth named after him, the Graham Farmer Freeway, which passes directly underneath the dodgy Perth suburb of Northbridge.  Good job too, because you wouldn't want to have to drive through Northbridge if you could help it.  The tunnel is known among your more humor-orientated locals as "the Polly Pipe."

Eddy Lincoln's proud papa,
shown here WITHOUT a hat.

On this day in 1846, famous beard and hat aficionado Abraham Lincoln became a father for the second time.  What a great man he was, who contributed so much to the world of public hat and beard wearing in spite of having such a miserable home life.  Even naming the child was mired in conflict:  "Eddy" versus the mother's irrational insistence on "Eddie."  What a nut-job that Mary Todd was!  But Lincoln's joy was to be short-lived.  Literally, as Eddy only lived to age three years, ten months and 21 days.  I cannot look at a  US one cent coin without seeing some of his anguish.

Also on this day, in 1947, famous Toledo resident Don Scholz became a dad!  This is wonderful news, because little Tommy did everything that typical boys do.  He fiddled with everything from go-karts to airplanes, was a basketball star in High School, took piano lessons, and went on to get a Master's Degree in Mechanical Engineering from MIT.  Don was incredibly proud of his boy Tom, but the best was yet to come.  After working as an engineer for a few years, Tom Scholz literally "gave up the day job" and founded one of the three greatest American Prog-Rock bands ever, Boston, and became a bazillionaire rock star!  Every parent's dream come true.

Founder of Boston born on 10 March.

(The other two are Kansas and The Mothers of Invention, in case you weren't sure.)

Many people misunderstand what it means when  father is "proud" of his boy.  They project their own insecurities onto the situation and assume that it is a kind of boasting, a self-validation, living vicariously, or the dad simply attempting to big-note himself for something the son has accomplished.  This is the wrong interpretation entirely.  That swelling in the chest that a father feels when his son makes good is pure joy from the knowledge that the boy has unlocked a little of his own unlimited potential and is experiencing some measure of fulfillment of his own life's purpose.  That's what every father yearns to be able to do.

On this day in 1964, a very lucky guy named Phil became a father for the fourth time.  Who exactly is this Phil person?  It's a little complicated.  His real name is Phillip von Schleswig-Holstein-Sonderburg-Glücksburg.  But he's not German as one might assume, he's actually Greek.  He married well, though, to an English gal named Elizabeth Alexandra Mary Windsor, otherwise known as Queen Elizabeth II of England!  Although the lad in question, Prince Edward, will never become king of England (I think even his Chauffeur is ahead of him in the succession line), Phil is still very, very proud of his boy Edward, Earl of Wessex.

Speaking of royalty, this is also the very date in 1845 on which Alexander Nicolaievich Romanov's life changed forever.  His son Alexander Alexandrovich Romanov born on that day succeeded him as Tsar Alexander III of Russia, but married the most unfortunately-named woman in History: Dagmar.

Karl Whilhelm Friedrich von Schlegel,
born 10 March 1772.

In 1772, on this day, Johann Adolf Schlegel became a dad for the second time.  Both his sons became important German scholars and philosophers, but the younger son born on this day was by far the shining star of the two.  Karl Wilhelm Friedrich von Schlegel achieved rock-star status among German intellectuals.  Of course today no one remembers exactly what their deal was, but at the time it was all terribly important stuff.


On this day in 1705, Johann Jakob Stöller (what an AWESOME name!) became father to a son who went on to do some tremendous things.  For example, he discovered Alaska.  No small feat, since Alaska is a frickin' huge, frozen object found way, way up there!  Young Georg Wilhelm also got a lot of animals named after himself, also as a result of discovering them.  I'm not sure how he missed out on naming rights to "Alaska" though.  So I'm going to start calling the place "Stöllerland" from now on.

March 10th was not really a wonderful day for one particular father, however. Jean Calas, a merchant from Toulouse, France, died on this date in 1762 at the hands of his torturers, fanatic Catholics (i.e. the French Government) who insisted that he had killed his own son.  In fact, the son had committed suicide, but out of shame the family tried to hide the fact, which led authorities to suspect the dad of filicide.  A terrible series of events, to be sure.  And as usual one with at least one positive outcome.  The famous French philosopher Voltaire, aka Françios-Marie Arouet, became interested in the case and through his incessant needling, haranguing and embarrassing the government, he succeeded in having the charges reversed posthumously.  He also secured a substantial payout for the bereaved and aggrieved family.  The government was thereafter a little more circumspect about torturing people to death whenever Voltaire was around.


On March 10, 1977, Astronomers announce that they have discovered a ring of debris around Uranus.

What's so funny?  It's a true fact.  Look it up.

On March 10, 1876, Alexander Graham Bell made the very first telephone call, to his assistant who it turns out was only in the next room over.  He was over-charged for the call, and is currently still on hold with customer assistance to try to get it resolved.

That means that as of today, the telephone has been around for 136 years.  But do you think my son will pick one up and call me?  Or is he going to wait another 136 years to talk to a dad who is very proud of him, no matter which nation or province he becomes supreme ruler over, how big a rock star he becomes or how many new species get named after him?

Son, you're always a star in my book.