How Science Works II: The Prequel.

Magnetism has been known to humans since ancient times.  Even Aristotle (600 BCE) speculated in his usual pointless way about the possible spiritual nature and moral implications of magnetism.  Little real progress was made in understanding the actual nature of magnets before 1820 when Hans Christian Oersted made the accidental discovery that a magnetic field can be created (!) by the flow of an electric current.  Up until then,  only "God" could create a magnet.

Of course nobody believed him until he actually proved it.  Current on: the compass needle deflected perpendicularly to the electric wire.  Current off: the needle resumed pointing north.  The Occam's Razor explanation (and there were no competing explanations even in the running that did not somehow involve fairies, magic, or other untestable nonsense) was that electric currents truly did create magnetic fields, every single time.  It was part of Reality.  It was an objective fact.

Shortly thereafter, André-Marie Ampère quantified the discovery by experimentally determining the relationship between electric currents and magnetic fields.  Rendered in English, the relationship goes something like this:  "A steady moving charge of J Coulombs per second must have around it a magnetic field the strength of which at any point is B.  The direction of B at all points is at right angles to the electric flow in the right-handed sense, and has a gradient (direction of most rapidly decreasing magnitude) that is kind of perpendicular-ishy to its own direction."

While philosophy students may argue endlessly about the meaning and accuracy of each of those words and the various implications and applicability of their sequence, the precise relationship is stated without any ambiguity whatsoever when the language of quantities is used:

.

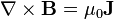This relationship predicts the strength of induced magnetic fields with an accuracy that rules out any other  relationship.  But is this just a convenient model for representing empirical data, or does it have a deeper meaning?

Just eleven years later, Michael Faraday made the unexpected reverse discovery that magnetic fields, when moving or changing, induce electric currents.  The exact quantitative relationship goes something like this: A magnetic field's time rate of change produces an electric field with a specific strength and spatial gradient that pretty much only a diagram full of wiggly lines and pointy arrows could adequately convey."

Mathematically, it is simply

.

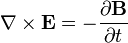And that was the state of Science in 1831.  Well, the science of electricity and magnetism, anyway.

By 1864, not much had changed and people still didn't know why these mysterious forces existed and what they were good for.  Much less understood was the mystery of why one natural force should be capable of creating the other, and why artificial man-made concepts like mathematical equations, of all things, should be so good at describing something natural.

In an attempt to plumb these mysteries, James Clerk Maxwell sat down to puzzle it all out.  He wrote down on his pad the equation for the relationship between electric charge and electric forces (Gauss' Law), the equivalent relationship for magnetism, the relationship between magnetic fields and electric fields (Faradays's law) and the relationship between electric currents and magnetic fields (Ampere's Law), which he then corrected to include the possibility that electric fields might sometimes be varying in time.  This is what he wrote:









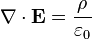
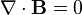
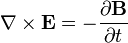
He decided to see what all these laws might imply when taken together.  This is only something that can really be done using mathematics.  But in English, the argument might go something like this.

"A changing magnetic field produces an electric field, which itself is necessarily changing and therefore produces another magnetic field, which itself is necessarily changing and produces another electric field, which itself is changing and produces . . . " and so on forever to infinity.

This "solution" to what are now known as Maxwell's Equations is mathematically in the form of sine or cosine waves and looks something like this:

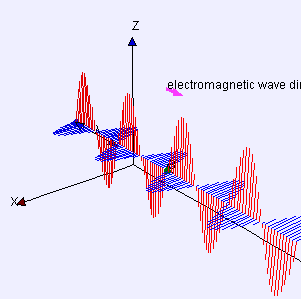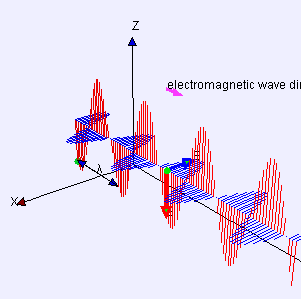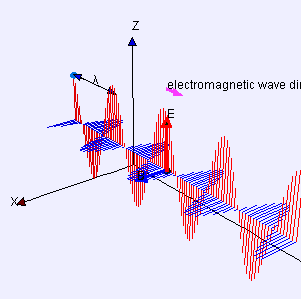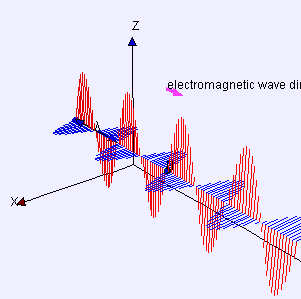Source: Wikipedia.  Red is the electric field, blue is the magnetic field.  And there
is something not quite right about this representation, but it's too
technical to worry about here.

According to Maxwell's Equations, these "waves" travel through nothing in particular at the curious speed



The speed of these "waves" is calculated as you can see from nothing besides experimental values of the properties of electricity and magnetism.  Its value is approximately 300,000,000,000 m/s or 186,000 miles per second.  Sound familiar?  Maxwell thought so, too. Because just two years earlier, an ingenious Frenchman named Leon Foucault (of pendulum fame) used an ingenious spinning wheel invented by an ingenious Englishman named Charles Wheatstone to determine that the speed of light was pretty close to 186,000 miles per second. Ingenious!  But is just it a coincidence?

Maxwell didn't think so either, but for a while he was quite alone.  What do magnets and wires have to do with light, anyway?  That's a totally different branch of physics.

But overwhelming empirical evidence soon forced the scientific community to accept "electromagnetic waves" as no mere mathematical artifact but as a proven reality.  The evidence was first provided by Heinrich Hertz 22 years later.  In 1886 He demonstrated irrefutably that electromagnetic waves A) existed and B) were in fact identical to the natural spectrum of radiation that includes all visible light.

Source: Wikipedia.  Visible light is a mere tiny sliver of the vast spectrum of electromagnetic waves.

What does this say about science and mathematics?  It is an example of how science, far from being just some kind of philosophy, is actually the gradually unfolding truth about nature.  It is the objective search for objective truth which, as a collective endeavor, inexorably overcomes individual humans' subjectivity, bias, assumptions, beliefs, ignorance and desires.  A group of philosophers, by contrast, can never become any smarter than they are at the start, no matter how much they argue with one another.

What this episode says about mathematics is even more profound.  What appears to many as a mere mathematical "trick" done by manipulating symbols according to arbitrary rules is actually something of far greater meaning.  Mathematics made the discovery of the true nature of light by showing that ordinary laboratory Electricity and Magnetism must necessarily also imply electromagnetic waves.  How did it do that?

Mathematics frees Reason from linguistic and cultural constraints and provides tools for feats of quantitative reasoning and logical analysis that would be impossible otherwise.  The connection was always there in the data, but no one could think linguistically all the way through the problem before.  Mathematics takes out all the ambiguities and allows the scientist to see things perfectly clearly in a way that nothing else can.

But wait!  There is something even more profound to learn.  If the mathematical forms of Faraday's Law and Ampere's Law were no more than good models of the data, basically "curve fits," then they could not have lead to a profound discovery that was not guessed nor even sought.  Maxwell's Equations were able to make such a left-field and totally accurate prediction, namely the unheard-of, undreamed-of existence of "electromagnetic waves," because those mathematical expressions represented something far more meaningful than mere formulas that happen to fit the data.

We might consider electromagnetism a "black box" that produces effects that we can measure and predict even though we don't actually knowing what's going on inside. Physical laws expressed in mathematical form represent not just the numerical form that empirical measurements are likely to take, but very accurately represent what is actually happening inside the black box.  That is the difference between a model and a Theory: a model need only reproduce results, but a Theory must provide an increased understanding of what is actually going on inside nature.  It must have the power both to explain and predict.

Ampere's Law and Faraday's Law are no mere models, but parts of an accurate theory of electromagnetism that at a deep level exposes how these two forces are actually different aspects of the same thing.  The Theory of electromagnetism so formed was true and powerful enough to lead us, without any further empirical input required, to a totally new discovery.  Namely, electromagnetic waves.

And that, my friends, is an actual, real and historical example of How Science Works and why Mathematics is its only useful language.


Stay tuned for Maxwell's Revenge: The Sequel to the Prequel!